Parallel Pathfinding with RRT* in Go

Project repo

Summary

This project focuses on creating a parallel maze solving program using the RRT* (rapidly-exploring random tree) algorithm. It has three run modes:

The program’s main() function takes input for creating the maze’s configuration space and executes the program either sequentially or concurrently through an ExecutorService interface defined in the concurrent package. The interface is implemented by the BSPExecutor and WorkStealingExecutor structs.

RRT*

The RRT* pathfinding algorithm is a random sampling-based motion planning strategy used in robotics to find optimal paths in high dimensional configuration spaces. For this project, the configuration space is a two-dimensional maze with a start point and end point. RRT* grows a path tree from the start point by randomly sampling points and extending the part of the tree closest to this new point by creating a new node called a milestone.

Each milestone has a cost that is set to its distance from the start point through traversal up the tree. As part of the input to this program, a “visibility” level is set that determines how far the tree can be extended in the direction of the new sample. A new milestone is a valid extension if the branch it creates does not pass through any obstacles (walls) of the maze. Validating a new milestone is a computationally expensive task that depends on how the configuration space is represented. For this program, each maze wall is a rectangle made of vertical and horizontal line segments. When adding a new milestone, collisions are detected by determining whether the line segment of the new branch intersects with any line segments of the maze walls.

Once a new milestone has been validated and connected to the nearest part of the path tree, RRT* attempts to rewire the tree near to the milestone. This involves a nearest neighbor search of the path tree, where a rewiring is performed if there is found either a more optimal path to the new milestone or the new milestone creates a more optimal path to another milestone. When an optimal parent to a milestone has been rewired, that milestone, and its descendants, require a cost update because they are now less distance to the start point. This is a recursive update and not very expensive, but if multiple threads are updating a large, complex tree, we need to ensure there is no conflict between the numerous recursive cost updates that may be occurring to large or small portions of the tree.

Once a path has grown to within a visibility radius of the goal point, the program tries to add the goal point to the tree by checking if any more optimal paths exist.

Mazes included in project:

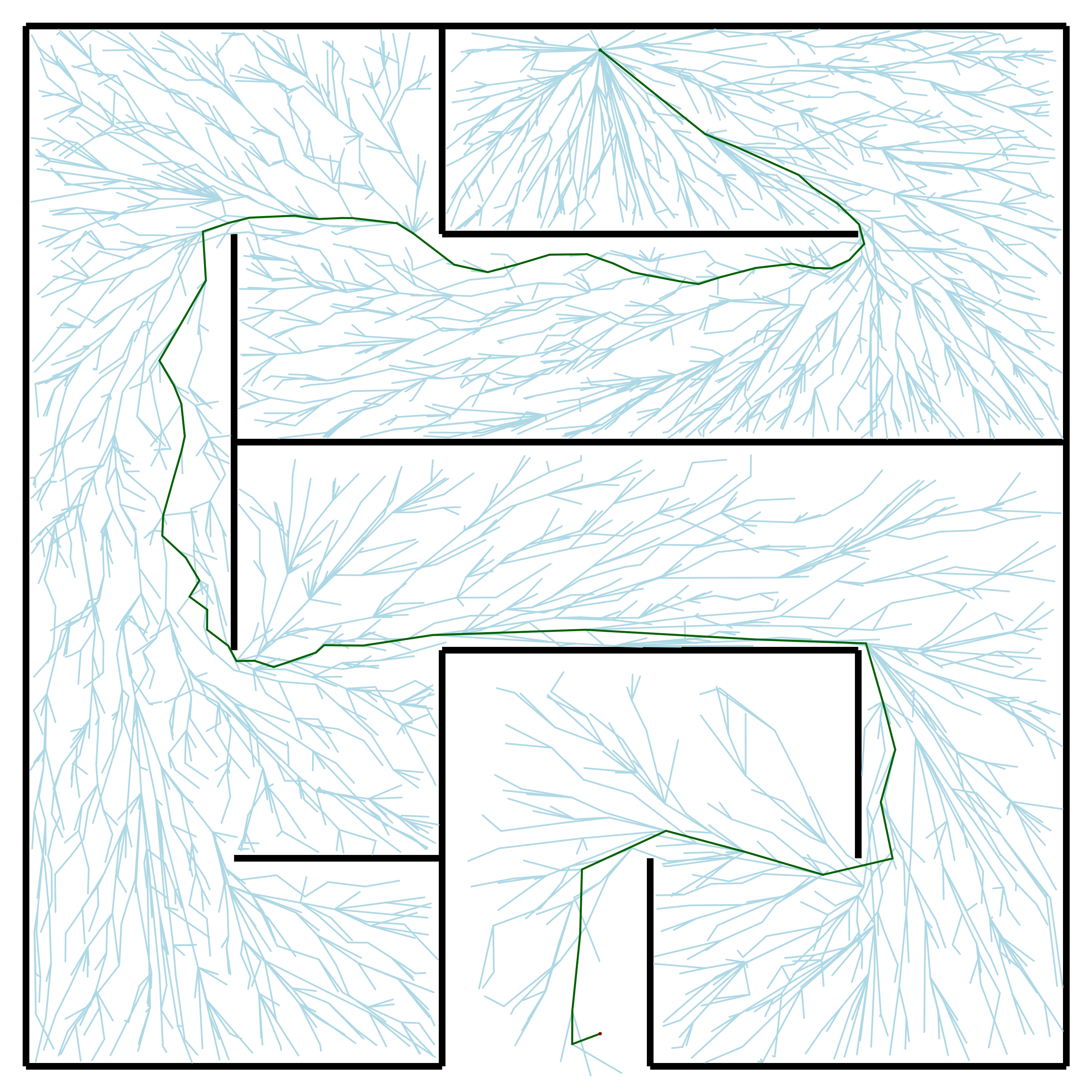
Extra-easy maze

Extra-easy maze (4,000 samples)

Easy maze

Easy maze (8,000 samples)

Medium maze

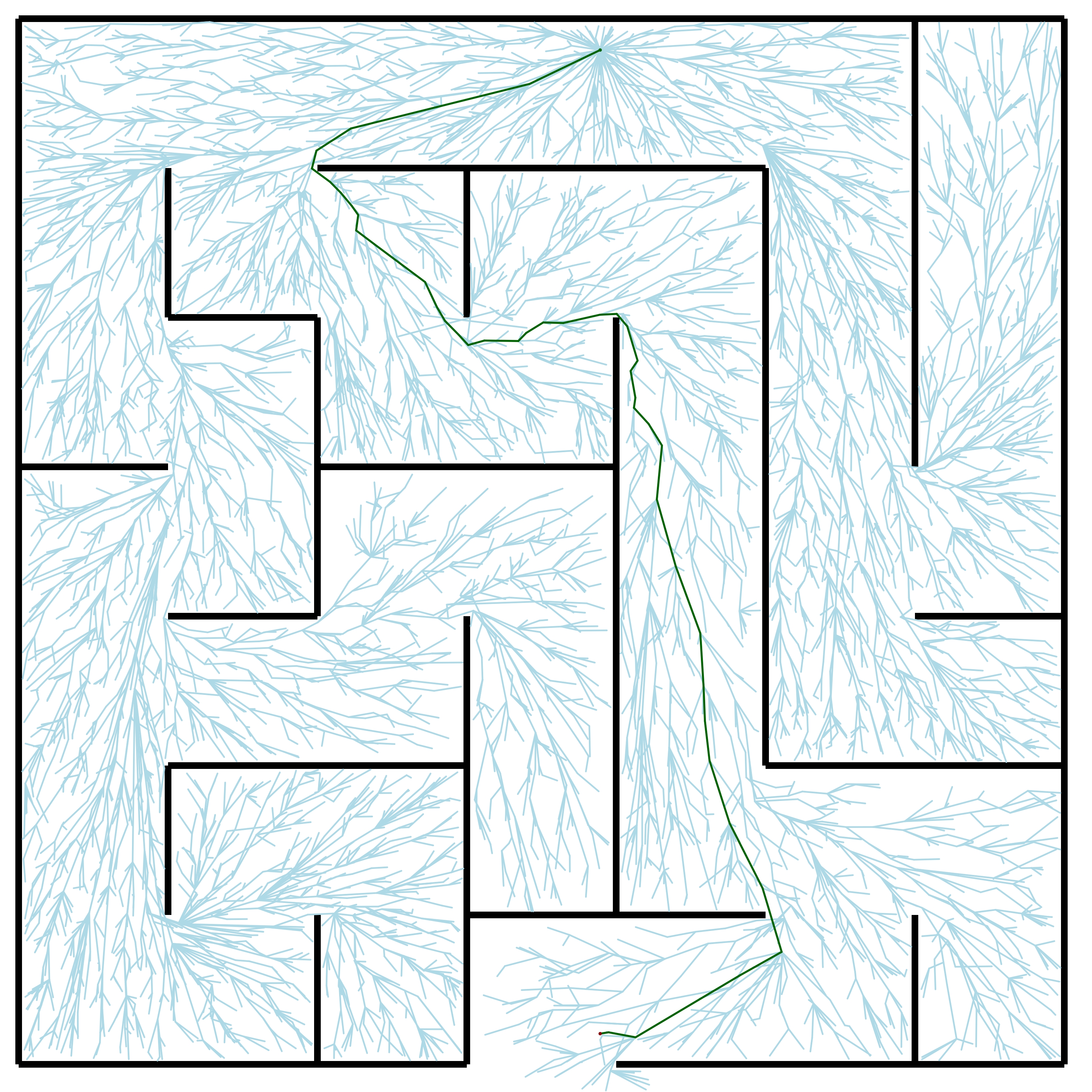
Medium maze (16,000 samples)

Hard maze

Hard maze (42,000 samples)

Parallel implementations

In the rrtstar package, this program parallelizes a single milestone update with the PathUpdate struct. In terms of implementation decisions, a milestone update was made parallelizable by several changes. A milestone is represented by the Milestone struct of the robotpath package, where a mutex is kept to update its cost and a concurrent map (sync.Map) is used to keep the milestone’s children. The path tree is represented by the Path struct and keeps a reader/writer mutex (sync.RWMutex) for accessing the slice that holds all the milestones of the tree. The read lock is used when determining nearest neighbors and the write lock is used when adding a new milestone to the tree. The slice is necessary because finding nearest neighbors through recursion down the tree is complicated with all the updates that could be occurring to the path tree. The function would need to progress down the tree through each milestone’s children map which itself could be undergoing an update during another thread’s rewiring of the milestone. A nearest neighbors search only needs to know what milestones are part of the path tree.

As a basic parallel executor, this program uses the BSP scheduling strategy. With BSP, I decided to define each step as creating a single milestone but not to update any milestone costs until barrier synchronization because every cost update locks the milestone it’s updating with a mutex, preventing rewiring by other threads. When adding a milestone, a cost update is only applied to the new milestone and its descendants after the optimal wiring has been determined. During the barrier phase, the costs are updated for each new milestones created in the superstep and all its descendants. This simplifies the recursive cost updates and should not have too great an effect on performance while the number of threads is not extremely large.

For the work-stealing executor, I implemented a concurrent unbounded deque that is local to each worker. The deque internally accesses a circular array to implement an interface with PushBottom(), IsEmpty(), PopTop(), and PopBottom() methods. The deque enqueues object references and is initialized with a capacity of 32. If PushBottom() finds that the deque has reached its capacity, then it calls an internal Resize() method. By using a circular array we avoid the ABA problem because the index for the bottom of the array cannot be reset while a thread is trying to pop from the top. The bottom counter will increase to the largest value permitted by its type and any popping from the top will fail if another thread has beaten it in the compare and swap.

A thread’s task is the same between both the BSP and work-stealing strategies with the exception of updating costs. In the work stealing implementation all steps involved with adding a new milestone using RRT*, including the cost update, are completed with the PathUpdate object popped from the deque. In the BSP implementation, the recursive cost updates are only completed after all threads have reached the barrier.

Creating the configuration space

When executing the program, the configuration space description is passed as a comma-separated .txt file.

The first four lines describe the space’s size (height, width), the visibility (radius) of a milestone, and the start and goal point locations (x, y). Following this, the configuration space’s obstacles are listed by their shape and location (currently the program only accepts rectangles). A rectangle is described by four values: top left corner’s x-value, top left corner’s y-value, height, and then width.

sampleInput.txt

window,3000,3000
visibility,100
start,100,100
goal,2900,2900
rectangle,300,500,2000,2400

To create mazes of varying difficulties, this project used the maze generator at www.mazegenerator.net . The website creates custom rectangular mazes up to 200 cells wide. The output is a .svg file that can be converted to the format above such that each wall is a rectangle. For this program, mazes of varying difficulty were tested. A 5x5 celled maze was designated as extra-easy, a 7x7 celled maze as easy, a 10x10 celled maze as medium, and a 15x15 celled maze as hard.

To maintain consistency between the tests, the mazes used in the benchmarking below all have a square window sized 3275x3275, a visibility radius of 100, and walls that are 20 grid squares wide. The number of samples required for RRT* to consistently solve the maze were hard coded into the benchmarking script, but these numbers can be changed when running the program normally.

Executing the program

The program runs in two modes, benchmark and simulation. The benchmark mode simply prints out the time it took to run given the arguments passed. The simulation mode draws out the result of the pathfinding and saves it to a jpeg. To save a picture of the result, make sure the data/output/ directory exists and install the required external drawing library:

mkdir data/output
go get -u github.com/fogleman/gg

To benchmark the sequential program using the example configuration space from above and 3,000 random samples, enter:

go run proj3-redesigned/pathfinder bench 3000 data/sampleInput.txt

To run the same configuration space and sample size, but with the work stealing parallel implementation, four threads, and an output picture of the simulation results, enter:

go run proj3-redesigned/pathfinder sim 3000 data/sampleInput.txt ws 4

The program’s full usage statement is provided by:

go run proj3-redesigned/pathfinder --help

Benchmarking results

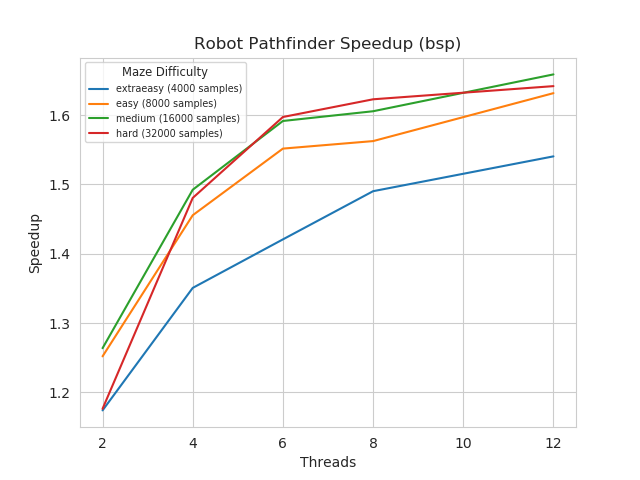
The speedup plots show that parallelization of milestone creation and processing using the BSP and work stealing strategies was successful. For the BSP implementation, the speedup ranges from about 1.2 with 2 threads to 1.6 with 12 threads. This is not surprising because the random draw and rewiring associated with a new milestone should not vary significantly once a tree has already started to grow and threads do not have to compete with one another much. This is likely the case once several hundred milestones have been created. After this, threads will tend to work on different parts of the tree and their time in completing each superstep will roughly be the same.

With the current implementation of BSP, threads reach the barrier and wait for the new milestone’s costs to be updated. The speedup for this implementation smoothly increases as the threads increase, reflecting the fact that each additional thread is mapped to a single task. The speedup realized is likely hampered because all threads share the path tree’s milestone array while processing their new milestone. Speedup would improve if we waited until the barrier synchronization phase to append the milestone array. This was the main challenge with implementing this strategy, separating out steps that would not intuitively be separated from the PathUpdate’s Run() method without breaking what “running” the update should accomplish with the other implementations. Additionally, more speedup could be had if we kept increasing the number of threads, as it does not seem an observable limit has been reached from this plot.

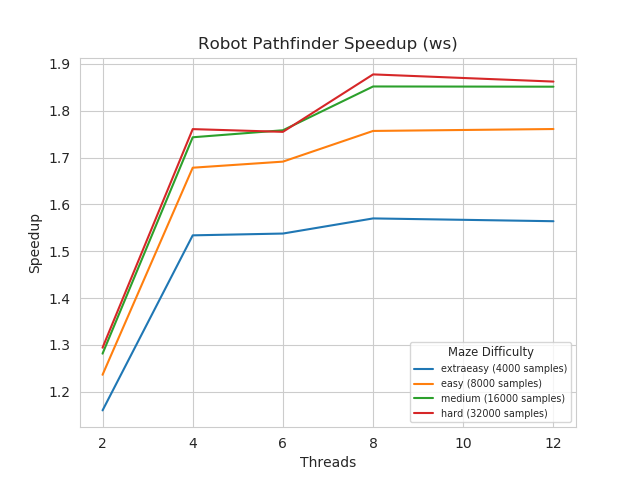
The work stealing benchmark plot shows evidence of even more speedup in parallelizing the RRT* algorithm. Over the different maze difficulties, the speedup ranges from about 1.2 with 2 threads to 1.85 with 12 threads. Although, it does appear that after 8 threads the speedup gained is minimal, perhaps suggesting that a limit with the algorithm is more quickly reached. The additional speedup over BSP could be attributed to the extra boost given by threads not needing to wait on barrier synchronization. So, when a particular milestone might take longer to complete, it does not hold up any other threads. Additional speedup may be had by tuning the work stealing algorithm further and adjusting hyperparameters such as the maximum tasks one thread can steal from another during an update, currently the number is set to 100.

For this problem, it appears that the work stealing implementation is more appropriate. The speedup is more quickly realized, which could make the difference if the program is run on a system with limited resources. To gain additional speedup by using BSP, there appears to be a more direct linkage to the additional resources needed, and this might not be the wisest choice when operating with robotics. If one prioritizes an optimal path and many samples are needed in creating this path, then these strategies both show that the process can be effectively parallelized. For both plots, as the sample size increased over the area of the window (all windows were the same size) the speedup increased. This is due to threads being less likely to compete with one another once the tree has become denser and more spread out.

Future improvements

There’s several areas where this project can be improved. RRT* is only one variant of many RRT related motion planning algorithms and it might not the most optimal or efficient for this specific application. Additionally, hyper-parameters such as the number of nearest neighbors used in rewiring and visibility radius of a milestone can have a large impact on the performance of the algorithm and speedup gained through parallelization.

This project’s base implementation of RRT* could also be made more performant through optimizations such as the use of a k-d tree in the nearest neighbor search, currently it uses a naïve search. Additionally, there are locks being set and concurrent data structures initialized in the sequential running that may have a slight overhead which is not accounted for. An entirely separate implementation would be necessary to separate the sequential and parallel versions.

It appears that the greatest limitation for the parallel implementations was the synchronization overhead created from the path tree’s shared milestone array used during the nearest neighbor searches. This would be challenge to further optimize as the nearest neighbor searches that use this array would need to remain consistent while new nodes were added by other threads.

References